
We have recently begun using the new ASH code to study full spherical shells of rotating turbulent convection. These 3--D simulations, using spherical harmomics Y_l_m (for horizontal expansion) up to degree l ~ 340, have attained a spatial resolution more than ten-fold greater in each dimension than those of the progenitor studies (e.g. Glatzmaier 1987). The model is intended to be a faithful if highly simplified description of the solar convection zone. Solar values are taken for the heat flux, rotation rate, mass and radius, and a perfect gas is assumed since the upper boundary of the shell lies well below the H and He ionization zones. The computational domain extends from 0.63 R_o to 0.96 R_o, where R_o is solar radius, thereby including a region of stable stratification of thickness ~ 0.07 R_o below the primary unstable zone in which effects of penetrative convection can also be studied. The shell currently has a density contrast across it of about 60, and thus compressibility effects are substantial. At this stage we must soften the effects of the very steep entropy gradient close to the surface that would otherwise favor the driving of very small granular and mesogranular scales of convection, with these requiring a spatial resolution at least ten times greater than presently available. The flux of enthalpy by unresolved eddies near the surface is explicitly taken into account, and thus contact is made with a real solar structure model.
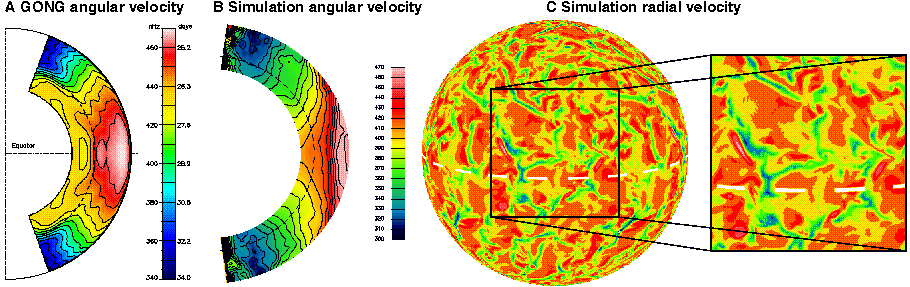
The resulting convection is highly time dependent and the flows are intricate. Figures 1b,c show properties of the resulting global-scale convection, and these are very encouraging when we consider the puzzle raised by helioseismology. In particular, Figure 1a contrasts the latest deductions about internal rotation rates obtained from an inversion of GONG helioseismic data (and Figures 2a,b in turn from SOI-MDI) with the time-averaged mean angular velocity obtained from the ASH simulation (Figure 1b). For the first time we are finding in these simulations, much as in the helioseismic inversion, that the angular velocity Omega is nearly constant on radial lines throughout much of the convection zone at mid latitudes, and that there is a systematic decrease of rotation rate with latitude in going from the equator to the poles (Elliott et al. 1998). In turning to the convective patterns, Figure 1c shows much less evidence of the earlier banana cells when viewing radial velocities near the top of the spherical shell. The convection is now dominated by intermittent plumes of upflow and stronger downflow, some possessing a distinctive cyclonic swirl, although there is still some semblance of north-south alignment of structures in the equatorial region. Most previous models yielded a fast polar vortex, in addition to Omega constant on cylinders aligned with the rotation axis. The shear layer of angular velocity speedup just below the surface at low to mid latitudes is not realized in our simulations, but that is a likely consequence of supergranulation effects which we currently do not capture. Further, the prominent tachocline at the base of the convection zone (below the dashed curve) is not realized in our simulations since they still operate at Reynolds numbers $R_e$ where viscous coupling can imprint the local rotation rate of the unstable zone upon the stable region. Some theoretical discussions concerning the tachocline (Spiegel \& Zahn 1992; Elliott 1997) invoke strong horizontal viscosity due to anisotropic turbulence in the stable layer to circumvent the diffusive spreading. Other models invoke magnetic fields to enforce solid body rotation in the radiative interior (Gough \& McIntyre 1998). Simulations at higher R_e (requiring greater resolution) and including the effects of magnetic fields can test such theories and provide hope for modelling the tachocline in the near future.

This page prepared by Nic Brummell, Laboratory for Computational Dynamics, University of Colorado.